La regresión es utilizada en todo tipo de industrias alrededor del mundo, es útil para predecir el valor de una propiedad inmobiliaria tal y como es útil para predecir el valor de un boleto de avión, las aplicaciones son infinitas. Casualmente también es la forma más sencilla y recomendad de entrar al mundo del Machine Learning, por este motivo es importante tener un entendimiento al menos básico de la misma. Para el final de esta publicación tendrás todo lo necesario para realizar tu primer modelo de predicción lineal con Python y sklearn (¡Incluyendo el código!).

En estadística la regresión lineal simple es un método matemático el cual estudia la relación lineal existente entre dos variables (de ser más variables sería regresión múltiple). Es importante destacar que la relación entre estas variables siempre será una relación estadística, es decir, no será “perfecta” o totalmente exacta, pero sí puede ser suficientemente cercana a la verdad como para ser útil.

La manera más sencilla de entender la regresión lineal es visualmente.

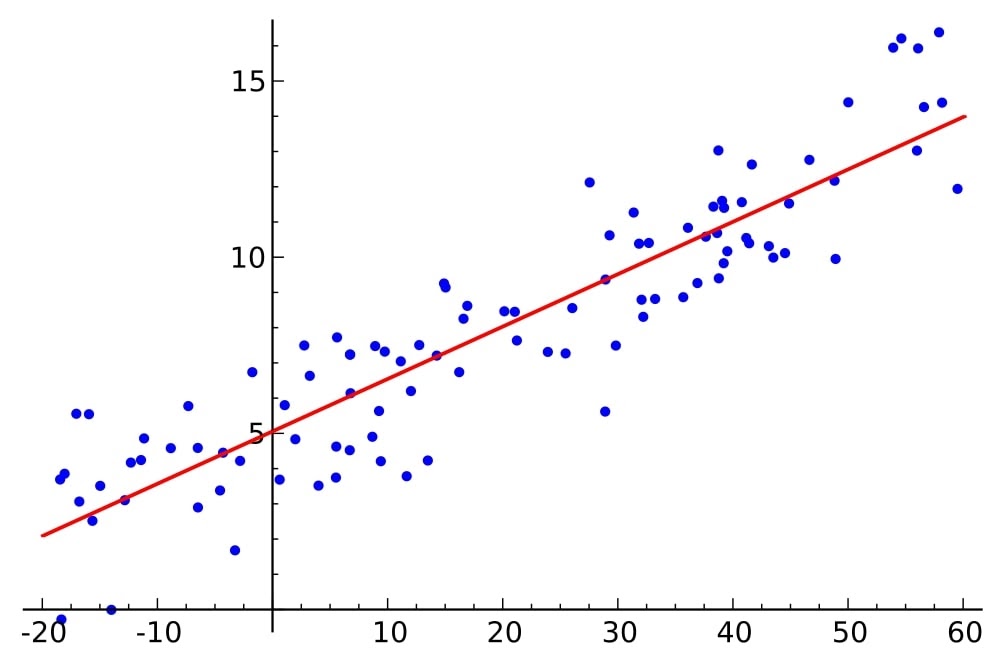
La anterior imagen muestra una serie de datos u observaciones representados como puntos en la gráfica. Es imposible encontrar una recta la cual pase por todos los puntos, pero si es posible encontrar la recta más representativa de todos esos puntos. Al encontrarla podría decirse que se está simplificando esta compleja nube de puntos en una sencilla recta.

Este artículo no detallará los métodos matemáticos necesarios para encontrar esta recta, ya que de eso se encargará Python, pero si se explicarán algunos conceptos básicos.

Rectas en pocas palabras

Una recta es una línea formada por una cantidad infinita de puntos a lo largo de una misma dirección (ocupando una sola dimensión). Toda recta puede ser representada mediante la siguiente ecuación:

y = mx + b

Además de las variables x e y tenemos la pendiente m y el término independiente b. La pendiente m determina la inclinación de la recta, si la inclinación es positiva podría decirse que la recta “va hacia arriba” mientras que si la inclinación es negativa “va hacia abajo”, lo cual no sería matemáticamente correcto pero si tiene sentido visualmente ya que leemos de izquierda a derecha.

Esta animación muestra el efecto de variar el valor m en la recta.

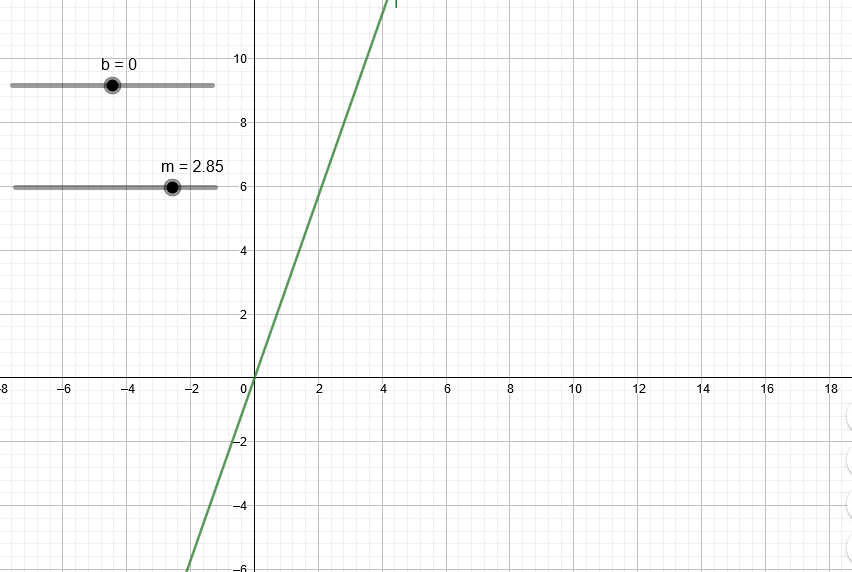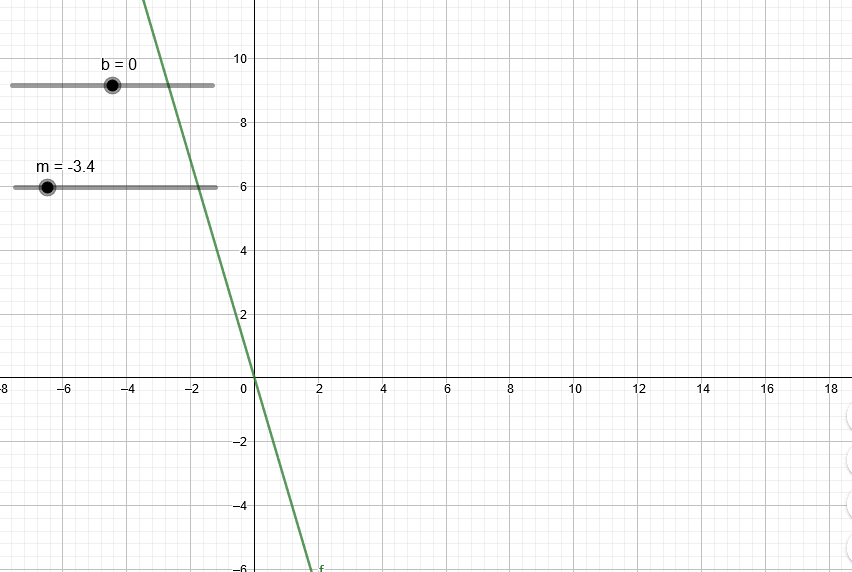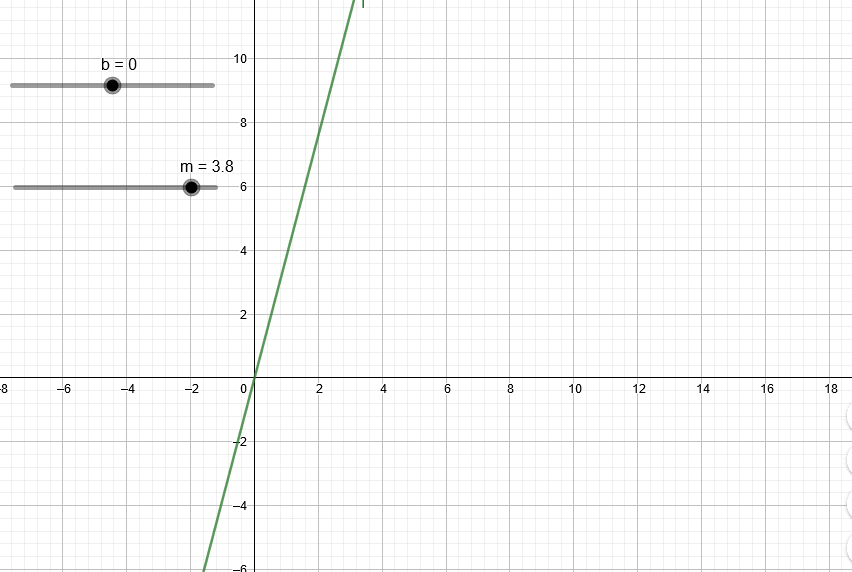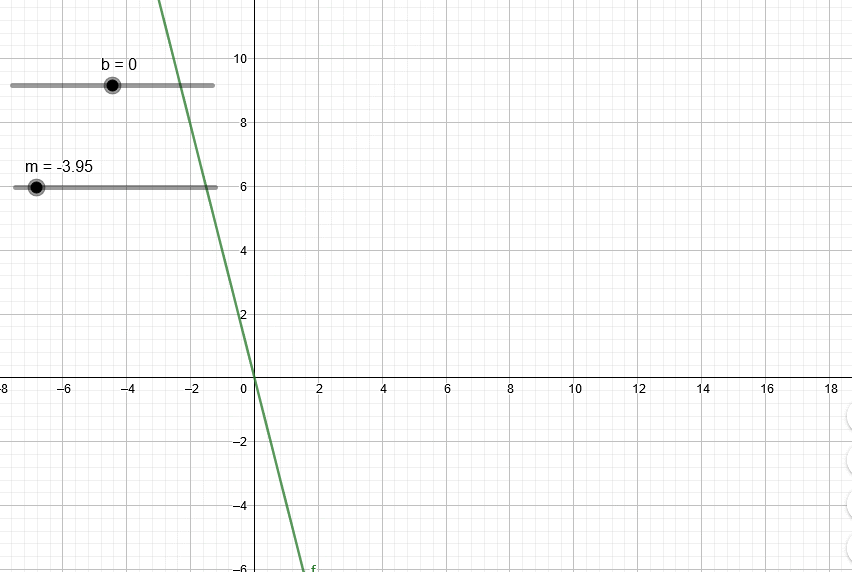
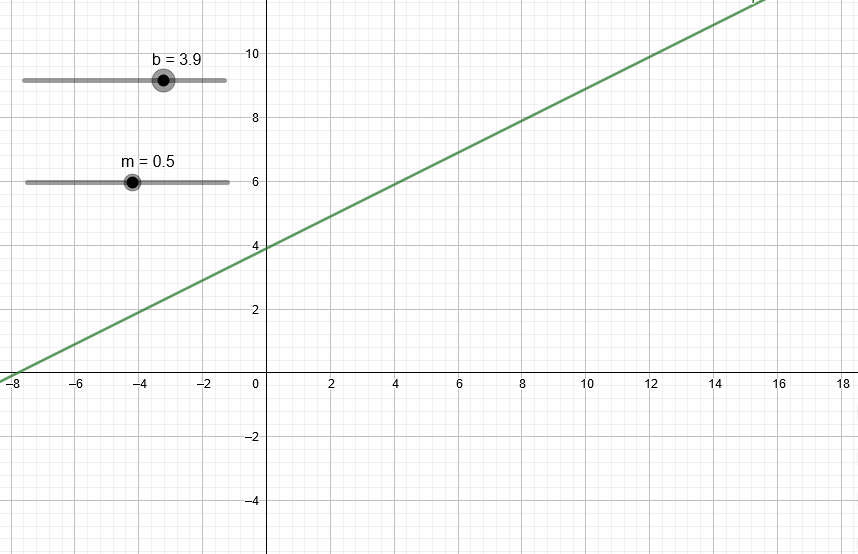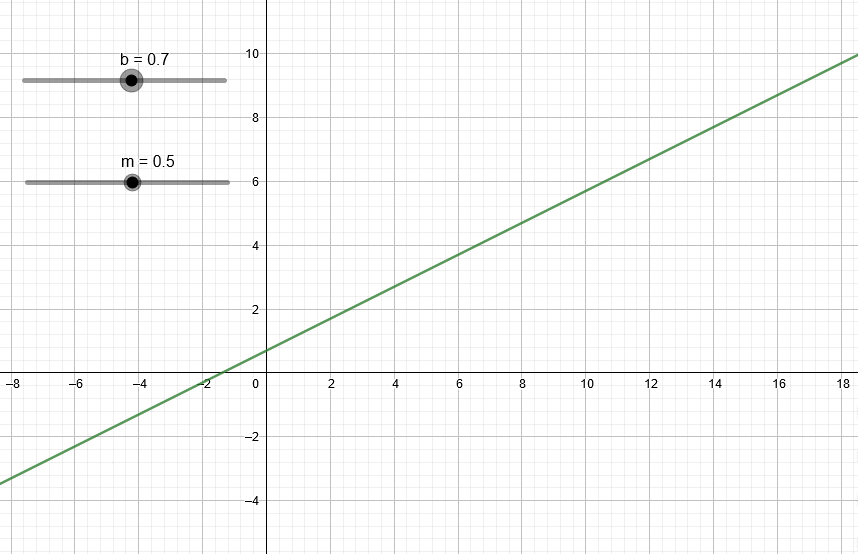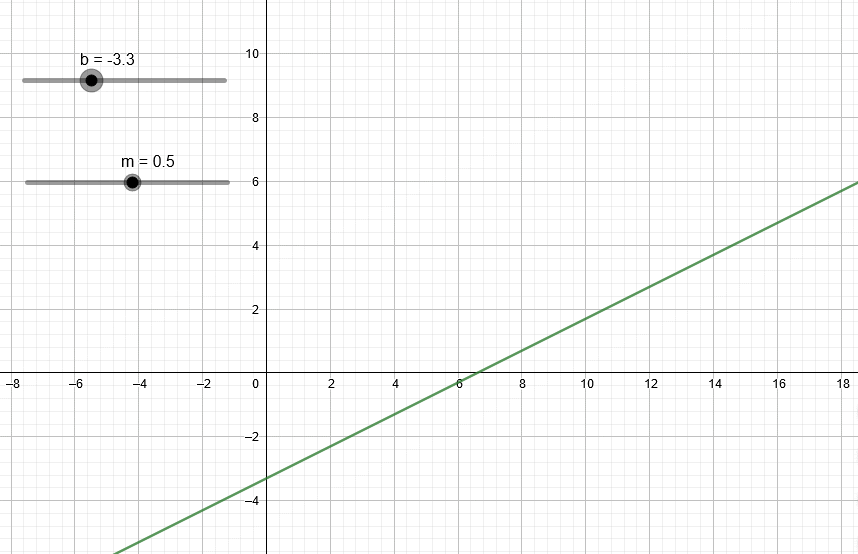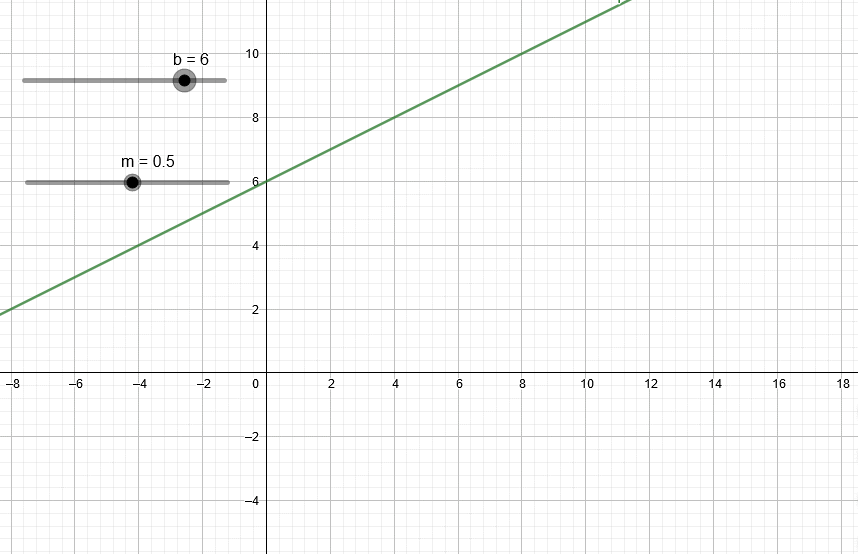
Esta animación muestra el efecto de variar el valor b en la recta

Métrica de error y R2

Como se mencionó anteriormente, las rectas obtenidas nunca serán perfectas, pero sí pueden ser útiles. Para juzgar su utilidad es necesario entonces calcular su error, es decir, que tan inexactas son. Para esto una de las herramientas más utilizadas es el coeficiente de determinación también conocido como R2score (en inglés) y comúnmente llamado sencillamente R2.

 El valor de R2 toma en cuenta la distancia de cada de los puntos a la recta, como se muestra en la siguiente imagen.

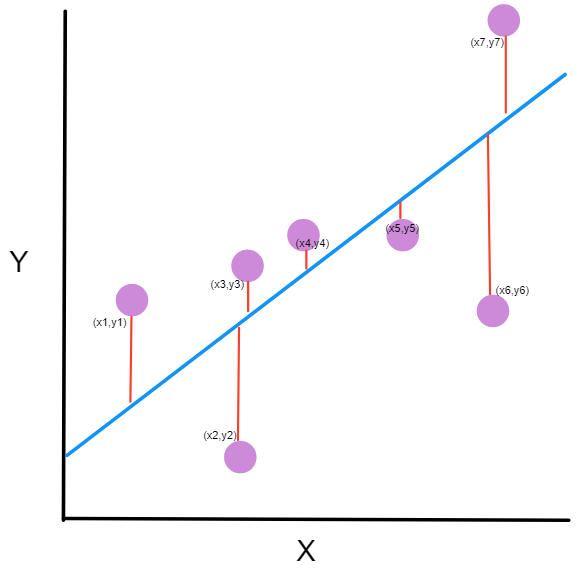
Si utilizamos entonces una regresión lineal para predecir un valor, el valor de r2 nos dice que tan confiable es esa predicción.

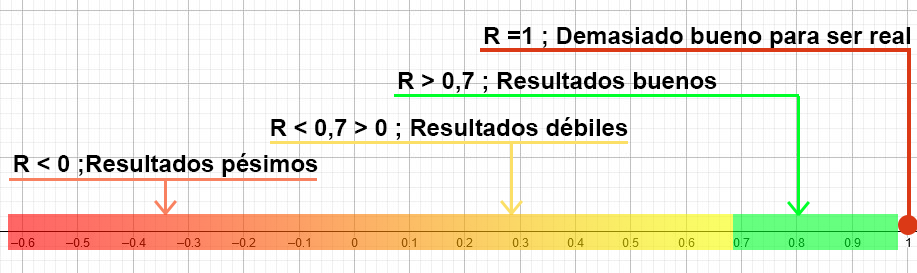
Significado de los valores de R2 en pocas palabras:

• 1 es el valor máximo posible, un resultado de 1 significa que la recta se ajusta perfectamente a los puntos. Esto es imposible en el mundo real y suele indicar que hay algún error en el modelo, se suele decir que este valor es “demasiado bueno para ser real”
• Un valor mayor a 0,7 significa que el modelo es bueno y útil la mayoría de los casos del mundo real.
• Un valor entre 0,5 y 0 es un modelo debido, probablemente no sea de mucha utilidad en el mundo real
• Un valor negativo da resultados pésimos.

Creando tu primer modelo

Ahora que sabes lo básico es hora d2e crear tu primer modelo. Por eso te invitamos a que abras este enlace de Google Colab, donde te mostraremos de forma interactiva cómo crear tu propia regresión lineal.

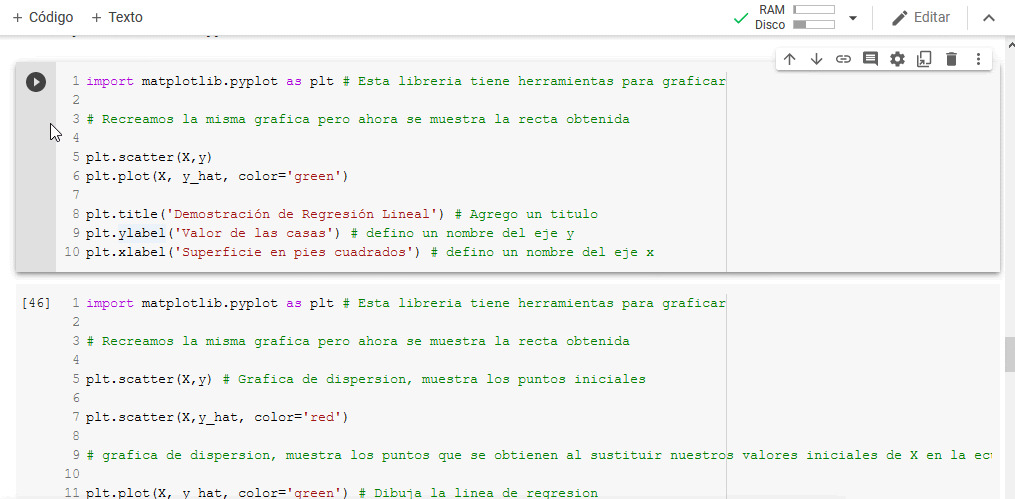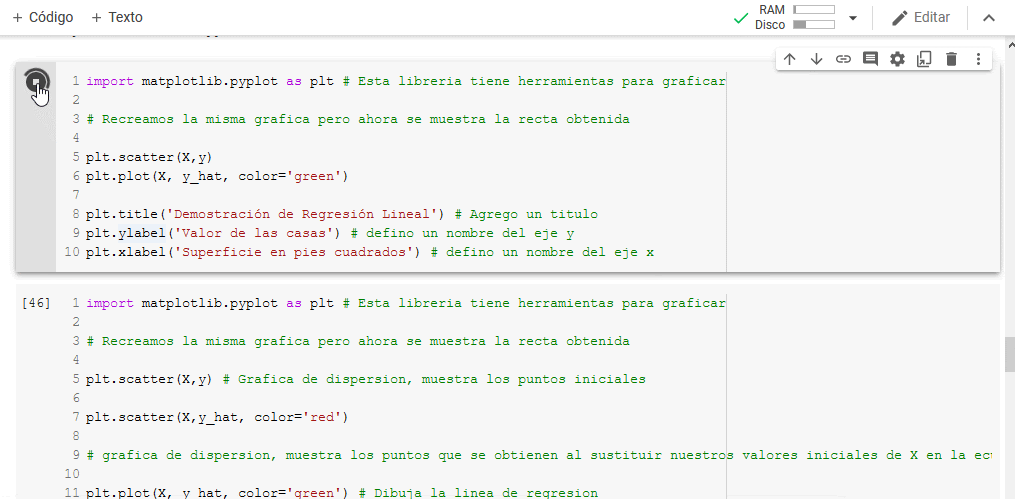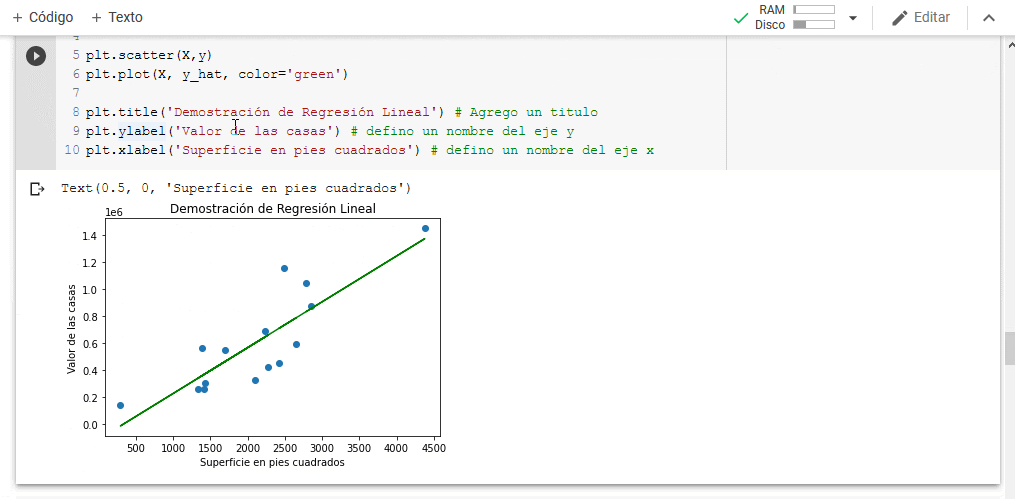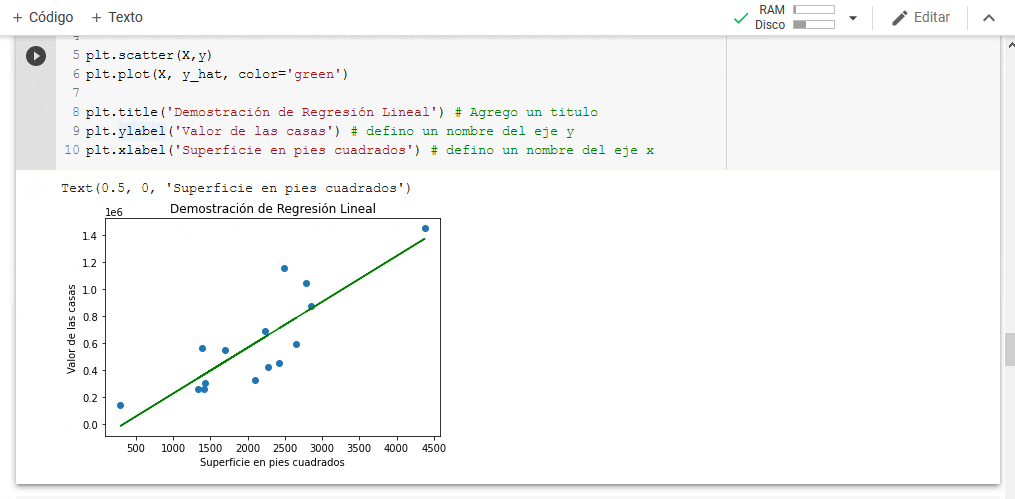
Google Colab es una herramienta que permite escribir y ejecutar código de forma colaborativa entre múltiples participantes, no requiere instalar ninguna aplicación ya que es 100% en línea y permite también ejecutar bloques individuales de código, con lo cual te mostraremos paso a paso cómo crear tu modelo.