IMPORTANTE: Este artículo es la continuación de este artículo anterior , es recomendable empezar desde el principio para entender bien los conceptos y poder seguir los ejercicios.

¡Armá tu primer modelo de Machine Learning! En esta segunda parte (primera parte acá)explicaremos de forma sencilla y accesible los conceptos teóricos básicos y haremos una demostración práctica (explicada paso a paso) sobre cómo armar un modelo simple de Machine Learning, el cual a través de regresión polinomial es capaz de predecir valores de casas en Estados Unidos simplemente conociendo algunos de sus datos. 

Vamos explorar los conceptos de polinomios (no hay que temer a la matemática, ya que Python se encargará de calcular) y regresión múltiple, además de la importancia y utilidad de separar el conjunto de datos inicial en conjuntos de entrenamiento y validación para poder evaluar la utilidad del mismo.

Polinomios y sus grados

Sin adentrarnos en demasiada matemática vamos a dar una pequeña explicación sobre los polinomios.

Un monomio es una combinación (expresión algebraica) de números y letras (variables) que consta de variables, coeficiente, y grado, estos distintos elementos se combinan exclusivamente a través de multiplicaciones. Esto puede sonar complicado pero es mucho más fácil entenderlo con un ejemplo. 

Es correcto afirmar que el monomio4x3tiene:

• Un coeficiente igual a 4
• Una variable x             
  
• Un grado 3                 
  

Un polinomio entonces, tal y como lo indica la palabra (“poli” significa “muchos”) es un conjunto de monomios.

Un ejemplo de un polinomio puede ser:

Podemos decir que el ese polinomio entonces está compuesto por 5 monomios distintos. Es importante notar que lo que separa un polinomio de otro son los signos de suma o resta. 

Para nosotros lo más importante de un polinomio es su grado. En el artículo anterior vimos que podemos representar cualquier recta con la ecuación:

y = mx + b

Según lo que acabamos de ver, mx + b es un polinomio de primer grado (ya que x elevado a grado 1 es igual a x). Igualando una variable y a polinomios de primer grado entonces podemos obtener rectas. Lo único que tenemos que variar es m y b, que si nos ponemos a pensar son coeficientes. 

Variando los coeficientes de una expresión de segundo grado podemos ver algunas de las parábolas que podemos obtener.

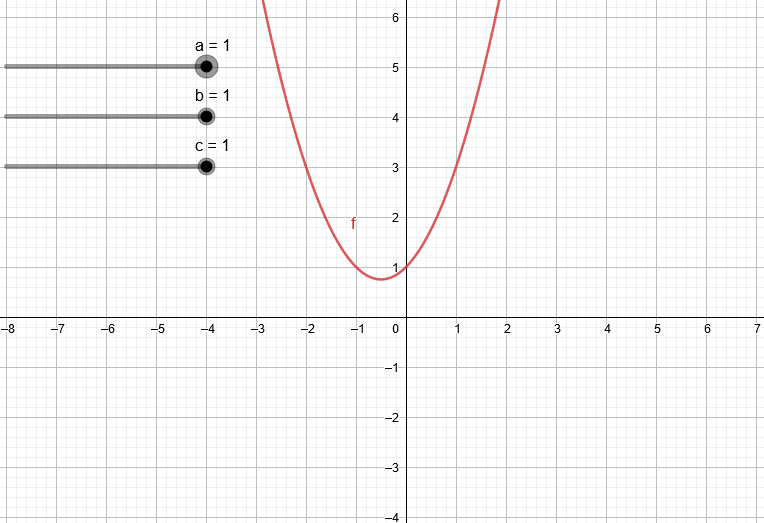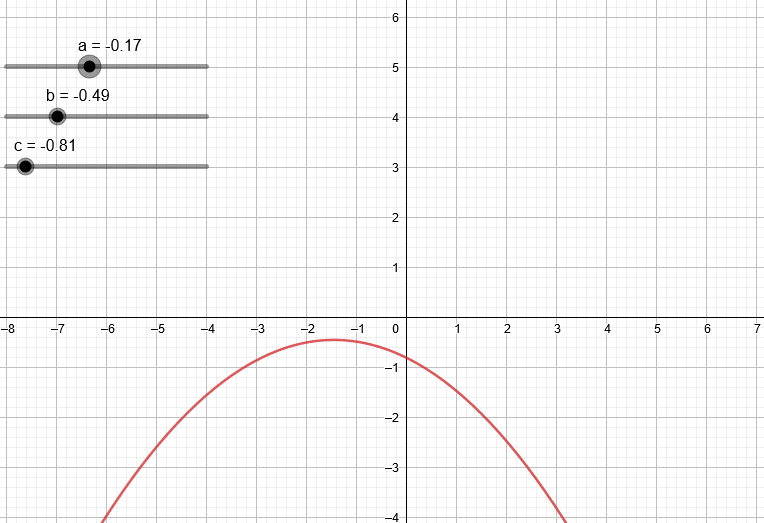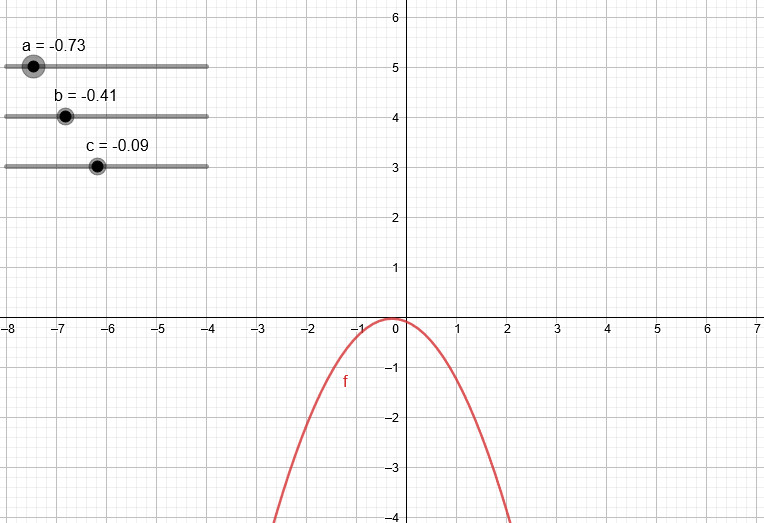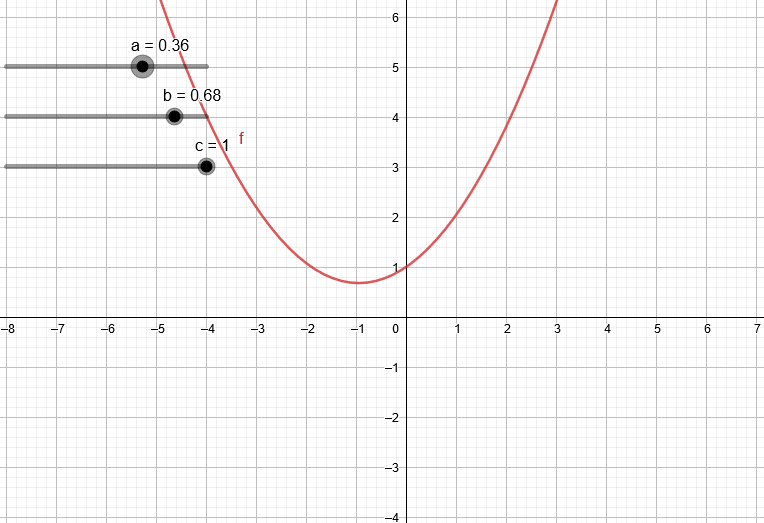
¿Qué pasa si trabajamos con un polinomio de tercer grado?

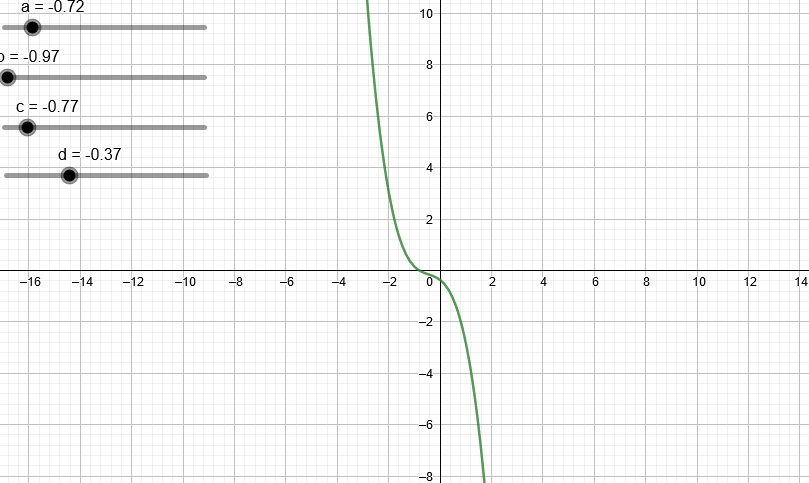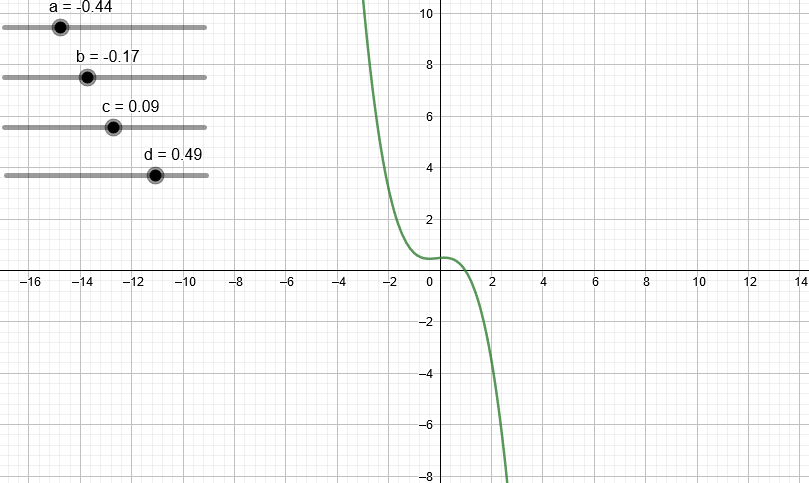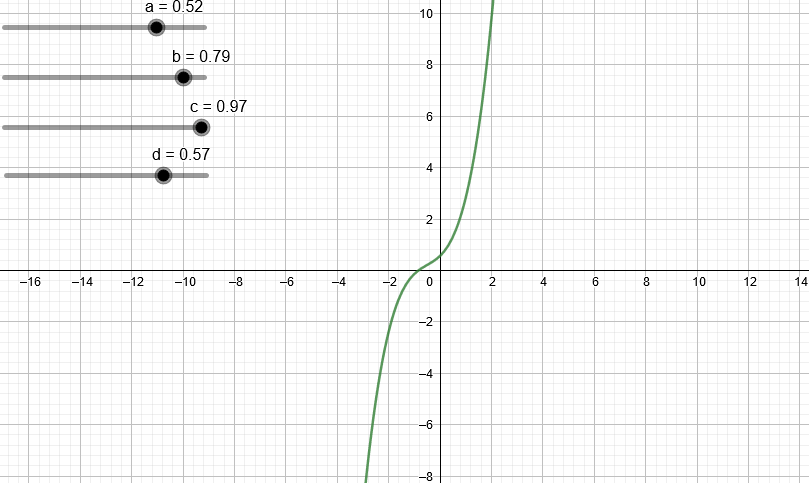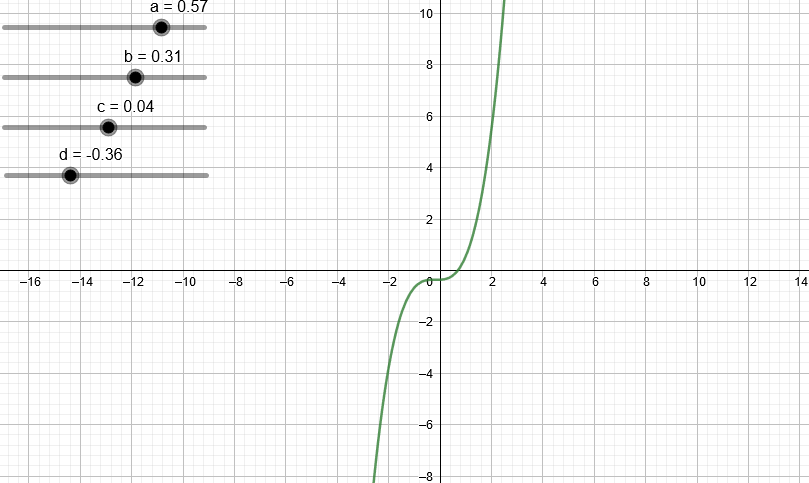
¿Y de cuarto grado?

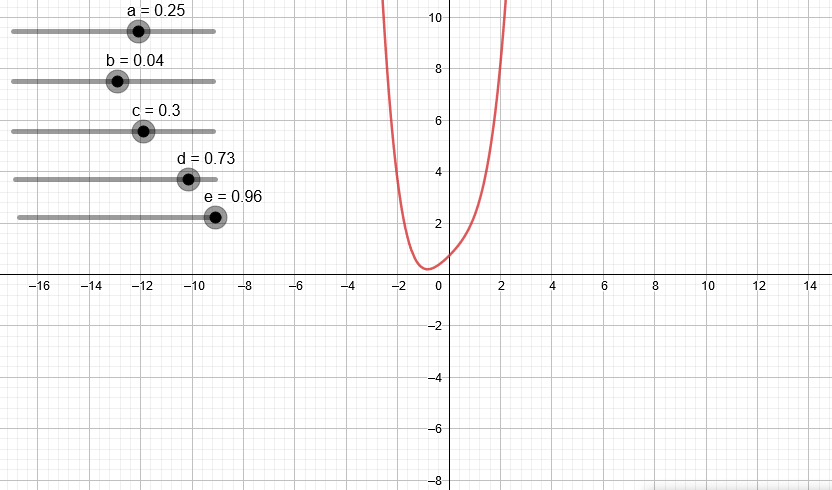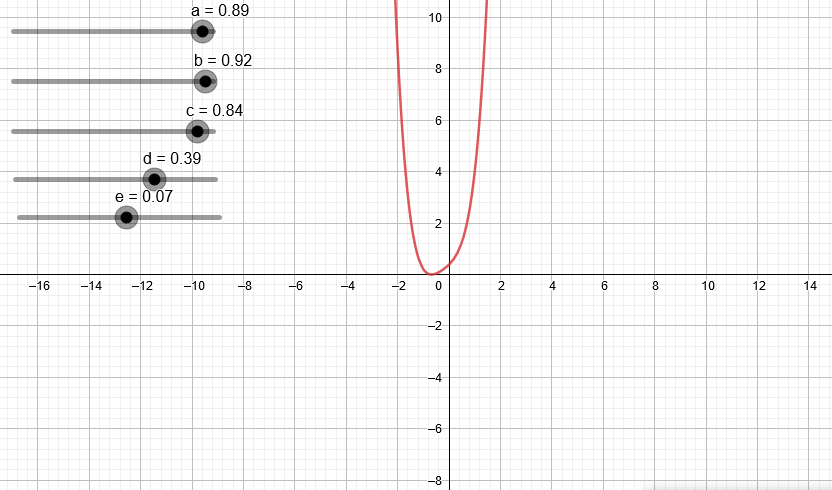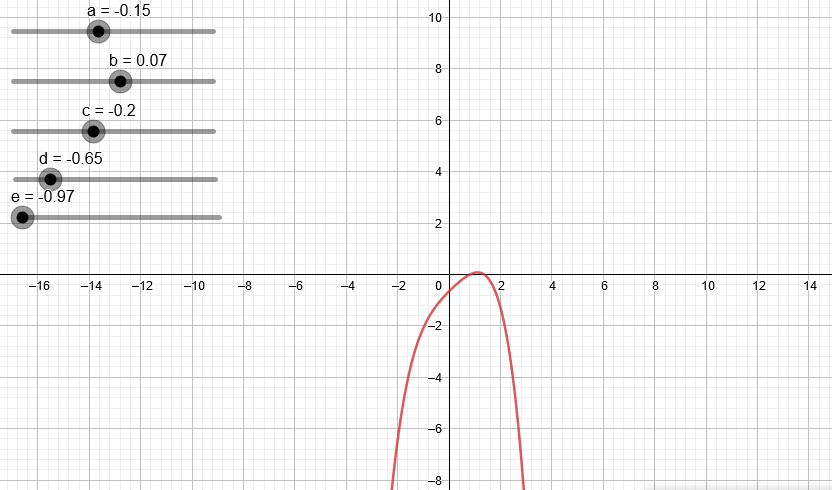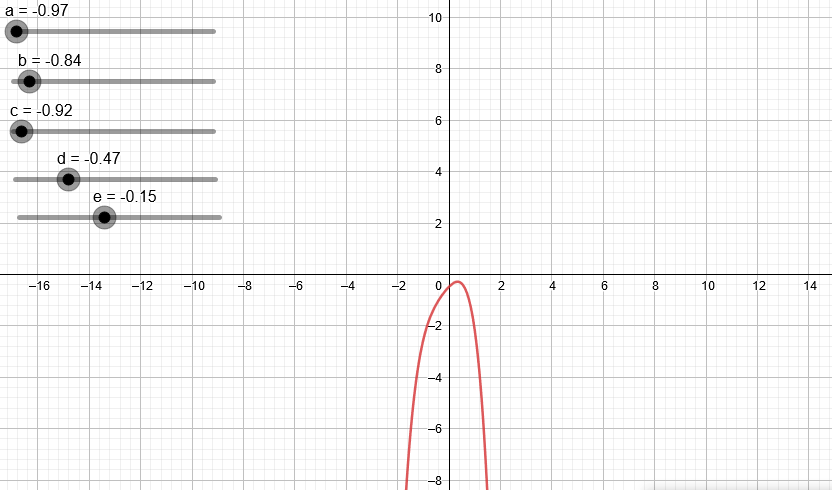
Podemos observar que a medida que aumentamos el grado del polinomio este puede “dibujar” cada vez más figuras.

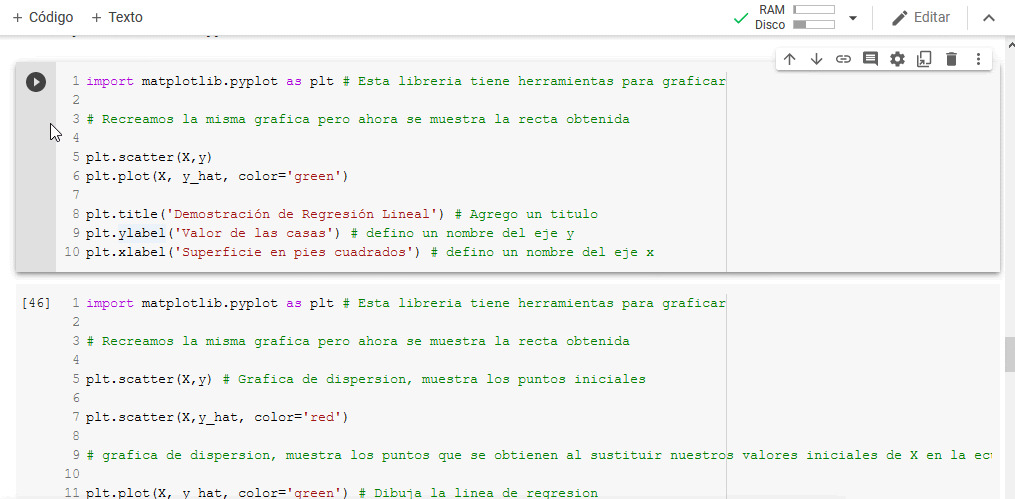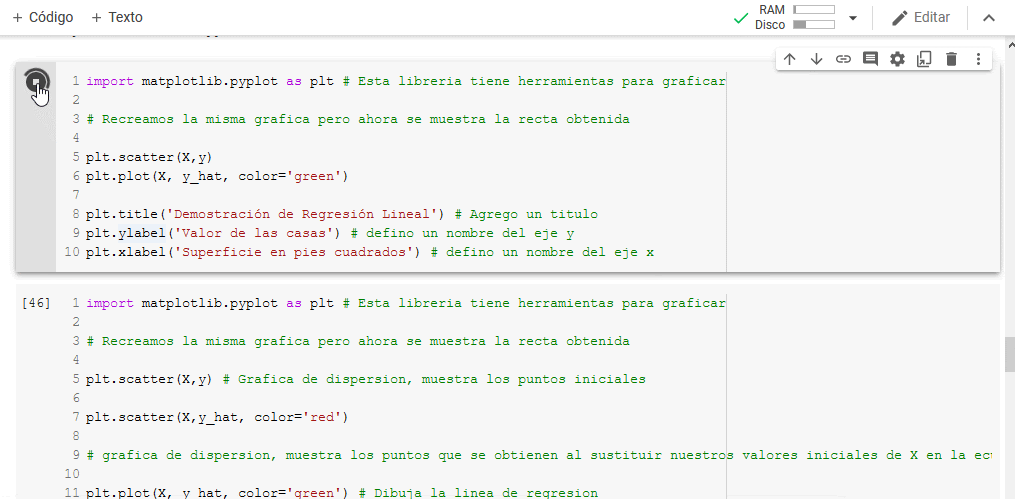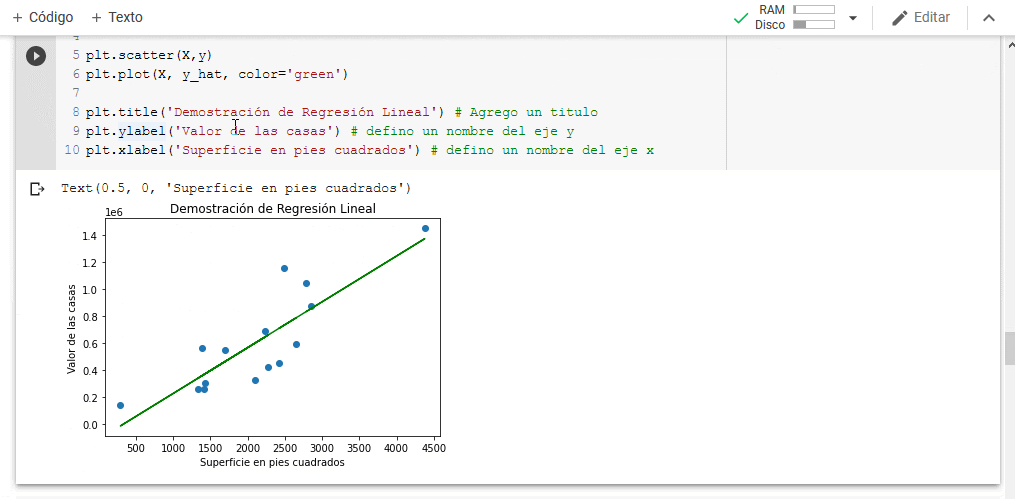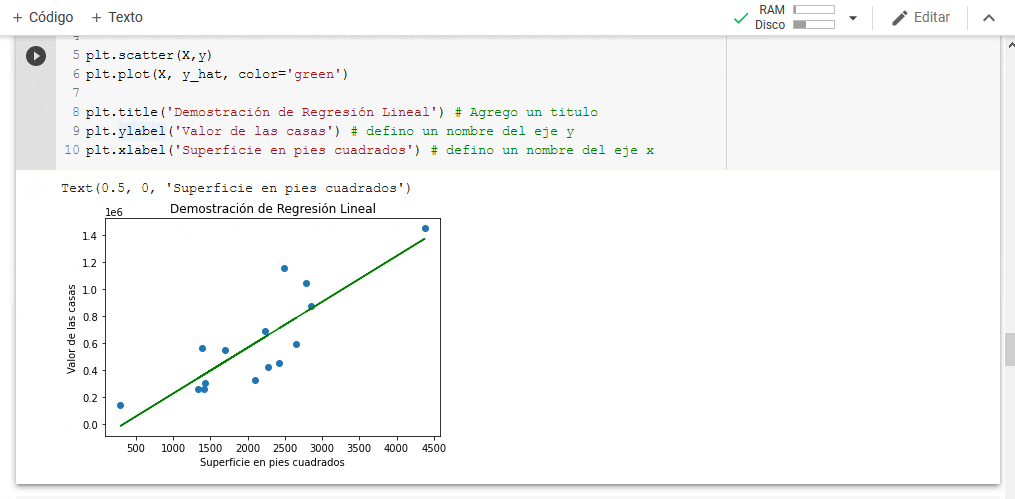
En el anterior artículo mostramos cómo hacer una regresión lineal, la cual básicamente intentaba resumir lo mejor posible una nube de puntos en una línea recta. En este artículo vamos a mostrar como obtener mejores resultados a través de una regresión polinomial, la cual según acabamos de ver puede “dibujar” figuras más complejas con curvas, dando un mejor resultado.

Regresión múltiple

En el anterior ejercicio concluimos que una sola variable no era suficiente para predecir el valor de una casa. Algo que sabemos de forma intuitiva en la vida diaria, todos sabemos que por ejemplo una casa en la playa suele ser más cara que una casa del mismo tamaño en otro lugar. 

Es necesario entonces recurrir a una regresión lineal pero con múltiples variables para evaluar si así conseguiremos mejores resultados. 

Un detalle que puede llegar a ser intimidante es el hecho de que al trabajar con más dos variables ya no es posible graficar nuestra regresión en dos dimensiones. En el ejercicio sencillamente nos guiaremos únicamente con el valor de R2 sin necesidad de graficar, ya que estas son exclusivamente para poder explicar de forma visual que está haciendo nuestro modelo, no son necesarias para el funcionamiento del mismo. 

La importancia de separar conjuntos de datos en validación y entrenamiento

En el artículo anterior mostramos cómo realizar una regresión lineal utilizando python, nuestra regresión lineal permite simplificar una nube de datos compleja en una sencilla recta. Es posible que hayas tenido que realizar ejercicios similares de forma manual en alguna tarea relacionada a física o química de forma de poder obtener el valor de una variable. La diferencia para este caso es que nosotros estamos interesados en crear una regresión la cual nos permita predecir valores, por lo que hay que tener en cuenta que el propósito de nuestro modelo es poder presentarle valores desconocidos fuera del dataset y que nos de resultados útiles. Por este motivo es importante no sólo utilizar métricas de error, sino que también mostrarle al modelo datos los cuales nunca ha visto. De esta forma, si las métricas de error nos dan buenos resultados con datos nunca antes vistos podemos asegurarnos de que el modelo verdaderamente está “aprendiendo” en lugar de solo “memorizando” y dará buenos resultados en el futuro. 

La separación de datos en conjuntos de entrenamiento y validación es siempre recomendable, pero es importante tener suficientes datos, ya que si nuestro dataset es muy pequeño, podría ser perjudicial el no estar aprovechando cada dato posible para entrenar al modelo. Como en el anterior ejercicio vimos que el dataset contiene miles de filas (o sea, datos sobre miles de casas), podemos entonces separarlo en dos conjuntos más pequeños. Normalmente se sugiere dejar el 80% de los datos de nuestro dataset para entrenar al modelo y el restante 20% para evaluarlo, llegando en algunos casos a dejar 70% del dataset para entrenamiento y 30% para validación en caso de que el dataset sea pequeño. 

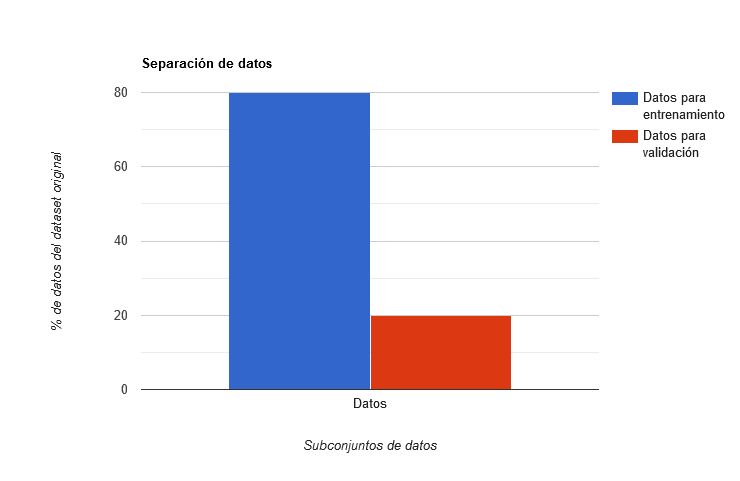
En resumen entonces lo que vamos a hacer en este ejercicio es separar nuestro dataset que contiene información sobre casas para obtener dos datasets más pequeños. Uno de estos datasets lo usaremos para entrenar al modelo mientras que otro lo usaremos para evaluar al mismo, similar a como un profesor plantea pruebas para sus estudiantes para evaluar su aprendizaje. Mediremos el R2 obtenido  con cada uno de los conjuntos de datos, obteniendo R2 en entrenamiento y R2 en validación. Siendo el R2 de validación con el que nos guiaremos para juzgar qué tan bueno es el modelo.

Te invitamos entonces a que vayas a este enlace de Google Colaboratory para ver de forma interactiva el ejercicio. Pondremos en práctica estos conocimientos obteniendo al final del ejercicio una regresión polinomial la cual toma en cuenta múltiples variables y evaluaremos sus resultados en los conjuntos de entrenamiento y validación. 

¿Qué es Google Colaboratory?

Google Colaboratory (Google Colab para los amigos) es una herramienta que permite escribir y ejecutar código de forma colaborativa entre múltiples participantes, no requiere instalar ninguna aplicación ya que es 100% en línea y permite también ejecutar bloques individuales de código, con lo cual te mostraremos paso a paso cómo crear tu modelo.