Introducción

Al momento de armar modelos de predicción podemos utilizar una gran variedad de técnicas, como redes neuronales, bosques aleatorios, regresiones, etc. Pero sin importar la técnica que usemos, no será de gran utilidad si no usamos buenos datos para entrenar el modelo.

Hay diversos factores que influyen en lo que podemos considerar “buenos datos”, en este artículo nos centraremos en uno de los aspectos más básicos: elegir las mejores variables.

Explicaremos de una forma accesible los conceptos de correlación y mostraremos ejemplos prácticos.

Un ejemplo de dataset (conjunto de datos) podría ser el siguiente, donde cada columna representa una variable.

Podríamos intentar usarlo para hacer un modelo capaz de predecir el valor de distintos pasajes de avión a partir de las otras variables.

Cuando usamos un dataset es poco probable que usemos todas las variables que vienen con el mismo, esto es porque algunas variables son más útiles que otras dependiendo de qué es lo que queremos predecir. Al punto de que la precisión del modelo puede bajar drásticamente si incluimos variables que no tengan una fuerte relación con la variable objetivo. Así que nuestro objetivo entonces es darle al modelo únicamente aquellas variables que mejoren su precisión. Por lo que surge entonces la pregunta: ¿Cómo sabemos cuáles variables son “mejores”?

Correlación

La correlación es una de las herramientas más útiles para poder elegir nuestras variables. La correlación es un concepto estadístico, lo cual implica matemática. Pero antes de entrar en pánico es importante saber que las herramientas de software se encargan de esta matemática por nosotros. Por lo que, con un entendimiento superficial es más que suficiente para comenzar a usar esta herramienta, aunque claramente el entendimiento matemático no le hace daño a nadie. Un aspecto importante a destacar es que por más que es muy útil, la correlación tiene limitaciones. Una de las más obvias es que al calcularse numéricamente, es imposible obtener la correlación entre una variable numérica y otra no numérica (un ejemplo de valor no numérico puede ser un color o una nacionalidad). Pero no te preocupes, en futuros artículos explicaremos cómo averiguar la relación entre estos tipos de variables.

La correlación se encarga de medir la relación entre dos variables, esto no implica necesariamente causalidad pero puede ser útil para predicciones. La correlación significa que dos variables tienen algún tipo de relación detectable, mientras que la causalidad implicaría que una variable influye directamente en la otra. Esto se entiende mejor con un ejemplo: Hace algunos años un estudio científico mostró que los niños menores de dos años que dormían con la luz encendida tenían mayores chances de sufrir de miopía. Estudios posteriores no encontraron ninguna relación entre luz nocturna y tendencia a sufrir de miopía, pero si demostraron que los padres que sufrían de miopía tenían una tendencia a dejar las luces encendidas durante la noche, además de eso, estudios previos también indicaban que existen predisposiciones genéticas a sufrir de miopía (es decir, es normal heredar). Con este ejemplo observamos que claramente hay una relación entre niños menores de 2 años durmiendo con la luz encendida y la miopía, pero esto no significa que la miopía sea causada por dormir con la luz encendida. 

Hay varios tipos de correlación, la más utilizada es la de Pearson o lineal, seguida por la Spearman y Kendall. En este artículo explicaremos únicamente la primera.

Un rápido recordatorio

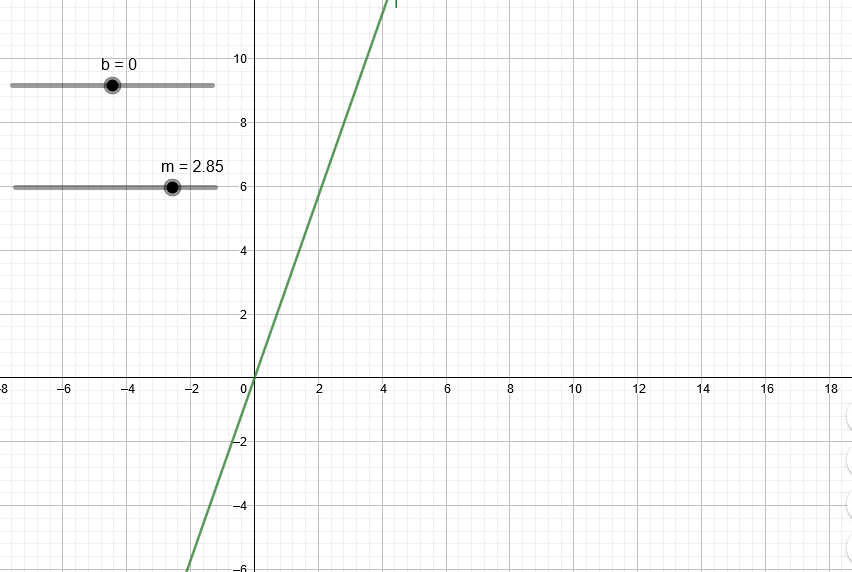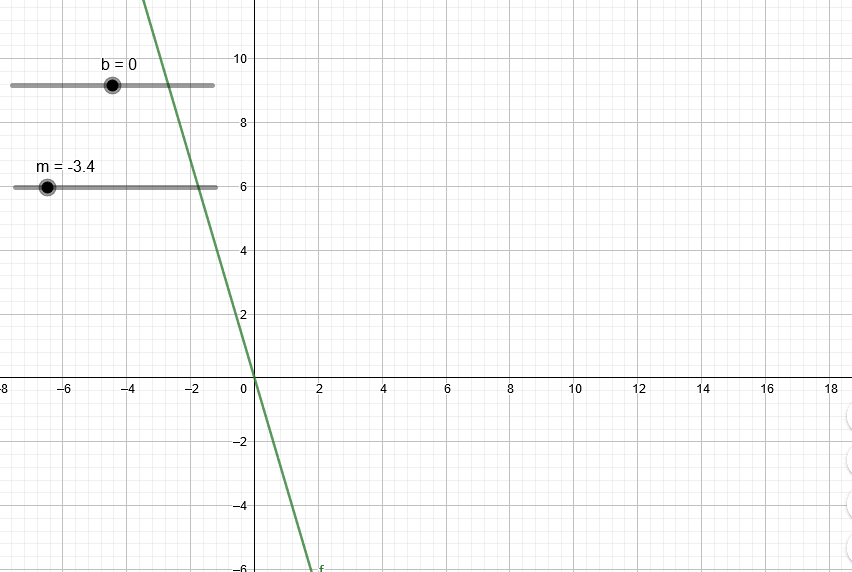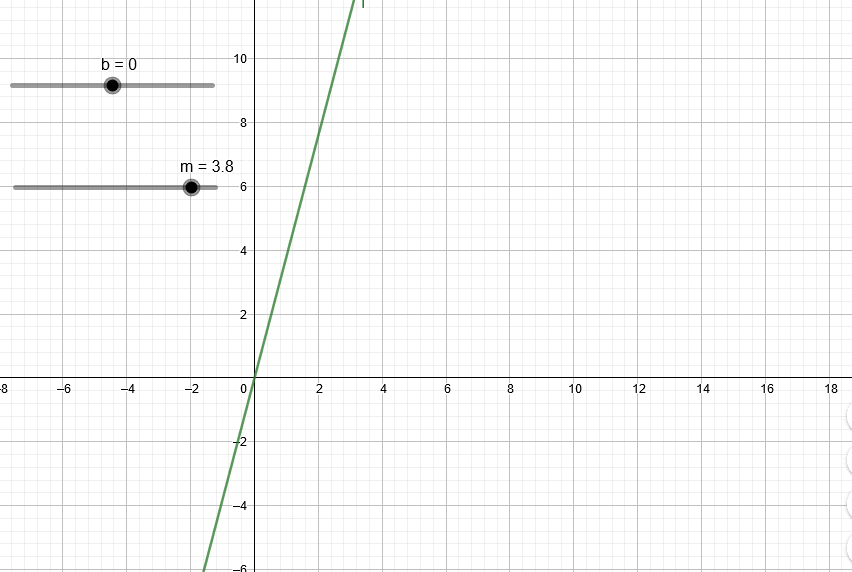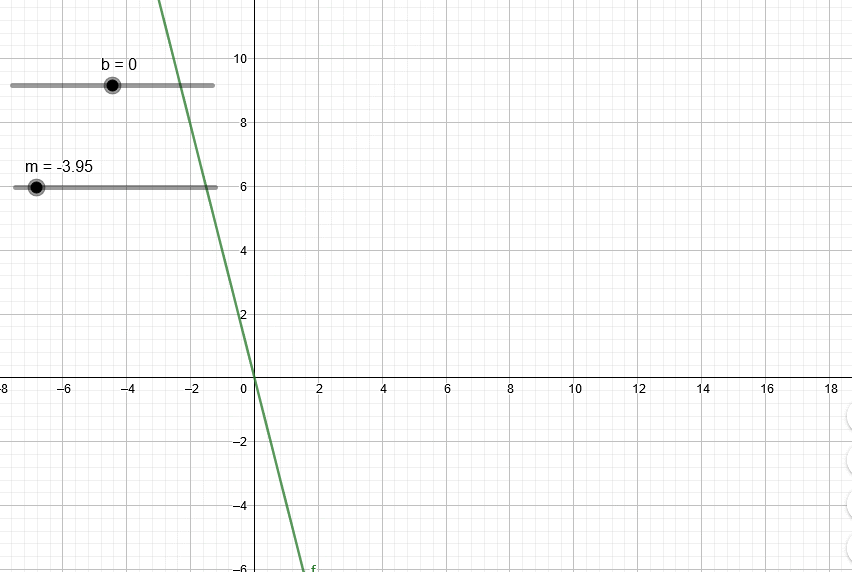
Si leíste el artículo sobre regresión, recordarás que toda recta tiene una pendiente. Si la pendiente es positiva la recta “irá hacia arriba” mientras que si la pendiente es negativa la recta “irá hacia abajo”. La siguiente animación muestra los efectos de variar la pendiente m (normalmente se usa la letra m para representar la pendiente).

Coeficiente de correlación de Pearson

La correlación de Pearson es la más intuitiva y sencilla, debido a esto suele ser la primera opción al medir correlaciones. Calcular el coeficiente de correlación de Pearson nos da un número que puede ir del -1 al 1. El primer valor indica una correlación perfectamente negativa, mientras que el segundo indica una correlación perfectamente positiva. Un valor de 0 por otro lado indicaría una correlación nula.

Si te interesa entender la matemática detrás del coeficiente de correlación puedes ir al siguiente enlace, pero este artículo se limitará a una explicación general, lo cual es más que suficiente para comenzar a armar tus propios modelos (e incluso para ganar desafíos en aiutechallenge).

La explicación sencilla es: si graficamos una variable en función de otra, entre más cerca estén los puntos de formar una recta más fuerte será la correlación de Pearson. Si esta recta imaginaria tiene una pendiente positiva, el coeficiente de correlación será positivo, mientras que si la pendiente es negativa el coeficiente de correlación será negativo.

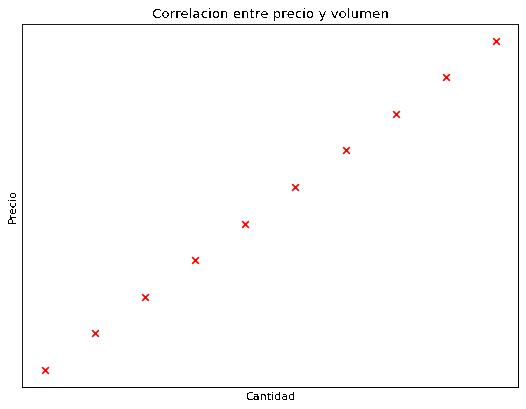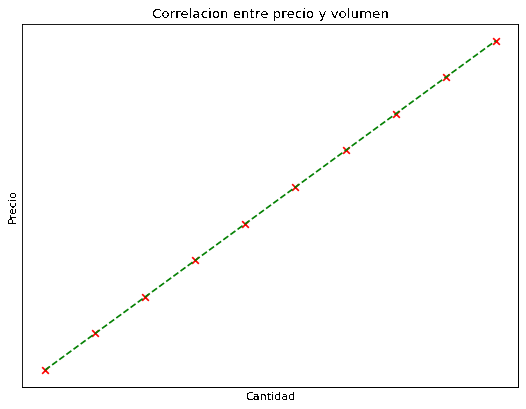
Por ejemplo, supongamos que vamos a comprar varias unidades de un producto con un precio fijo. Si graficamos el precio en función de la cantidad comprada deberíamos obtener una correlación perfecta como muestra la siguiente gráfica, los puntos están perfectamente alineados en una recta por lo que obtenemos una correlación de 1 (algo que nunca va a pasar en la vida real).

En el mundo real las cosas son un poco más complejas, generalmente comprar por mayor es más barato que comprar por menor, por lo que una gráfica más realista de precio en relación de cantidad sería la siguiente.

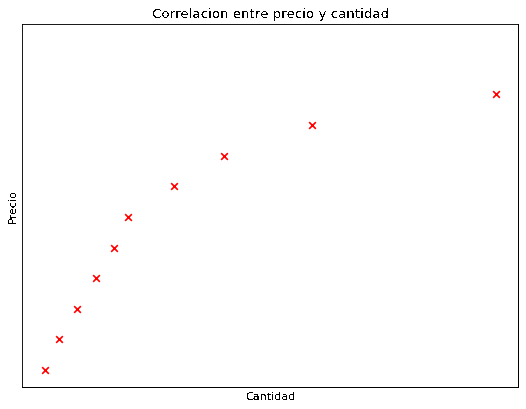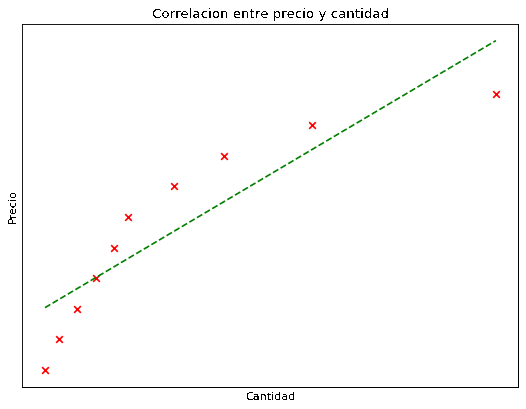
Vemos que ahora los puntos ya no encajan perfectamente en una recta, pero tampoco están tan alejados de la misma. Ahora entonces la correlación es alta pero menor a 1.

Esta imagen muestra varios ejemplos de los distintos valores de correlación (el valor de correlación está representado por el símbolo ) en distintas situaciones.

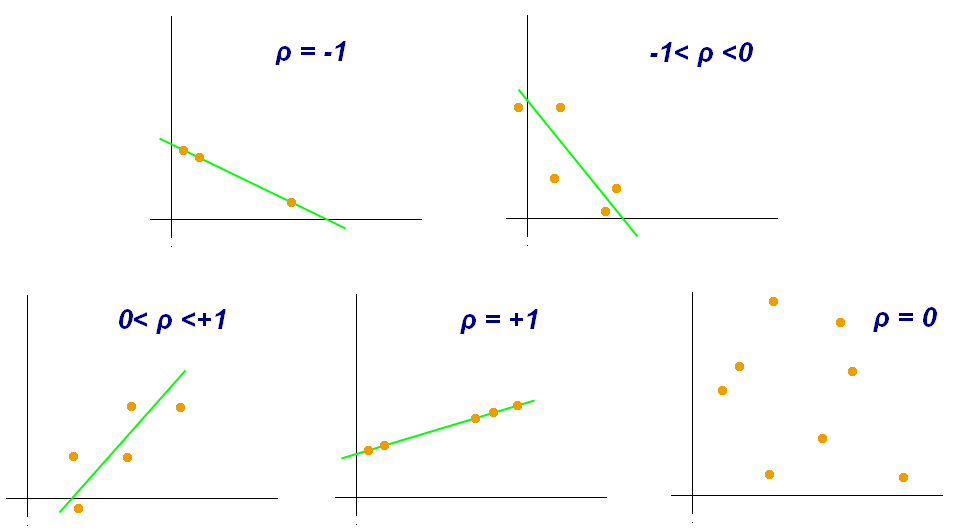
Vemos como para el ejemplo donde la correlación es cero, no hay ninguna recta. Este es el peor de los casos, donde no hay ningún tipo de correlación. Básicamente si sucede significa que la variable es inútil para realizar predicciones.

Decimos entonces que entre más cerca esté del 1 o -1 el valor de correlación la relación entre esas dos variables es más fuerte, debilitándose al acercarse al 0.

Generalmente para un modelo de predicción es útil usar variables con correlaciones mayores a 0,7.

Una rápida demostración usando la librería de Pandas

A continuación daremos un ejemplo rápido de como usar la librería Pandas para ver la correlación entre variables. Si quieres probar ese código tú mismo (también muestra cómo armamos las dos primeras gráficas) puedes acceder a este Google Colab y realizar una copia del mismo. ¿No sabés qué es Google Colab? Clickea aquí para aprender en 5 minutos.

La librería Pandas es una librería de Python muy utilizada para el manejo y análisis de datos. Pandas trabaja con dataframes, una palabra elegante para referirse a tablas como esta.

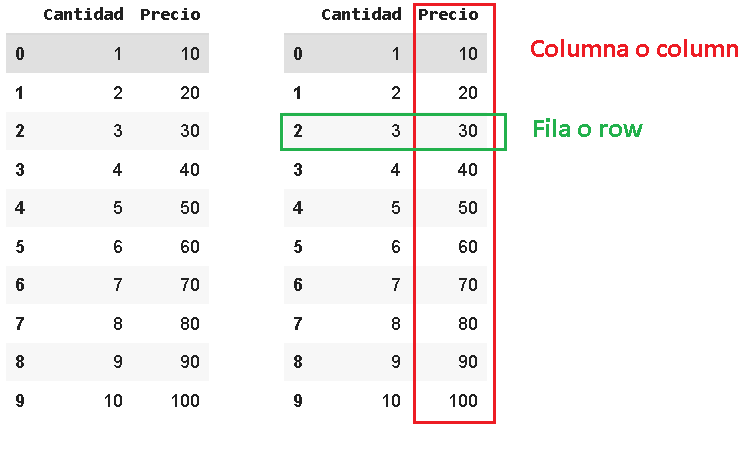
Para este ejemplo tenemos dos dataframes con distintos precios y cantidades, tienen los creativos nombres de df1 y df2.

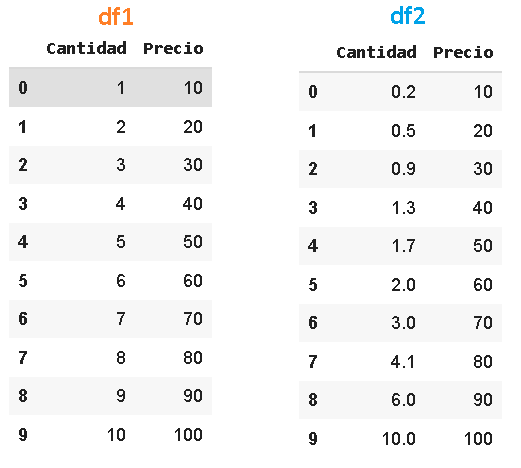
Pandas tiene la función corr() para medir la correlación entre las variables de un dataframe. Esta función permite elegir entre las correlaciones de Pearson, Spearman y Kendall. Podemos especificar que tipo de coeficiente de correlación queremos calcular de esta forma

mi_dataframe.corr('tipo_de_correlacion') 

Si no especificamos el tipo de correlación se usará por defecto la de Pearson.

Por lo que esto:

mi_dataframe.corr()

Es lo mismo que esto:

mi_dataframe.corr('pearson')

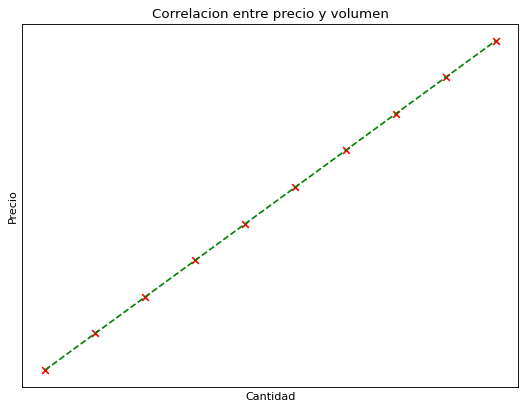
Al graficar el contenido de df1 obtenemos esta gráfica que mostramos anteriormente.

Por lo que, sabemos que al calcular la correlación deberíamos obtener un valor de 1, ya que los puntos encajan perfectamente en una recta de pendiente positiva. Cabe destacar que esto jamás sucederá en la vida real.
Calculamos entonces la correlación de esta manera:

df1.corr() 

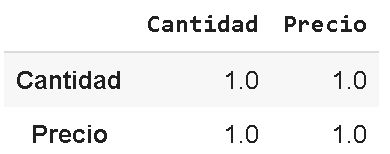
Y obtenemos la siguiente matriz que confirma la correlación perfecta. Vemos que la matriz también compara las variables con sí mismas, lo que siempre dará un valor de 1.0

Por otro lado tenemos df2, el cual al ser graficado da esta otra gráfica que ya mostramos anteriormente.

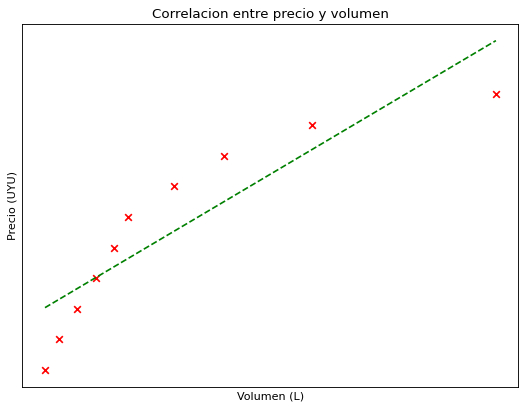
Al ejecutar 

df2.corr() 

Se obtiene esta matriz, con un valor de correlación entre precio y cantidad menor a 1, pero aún así bastante alto.

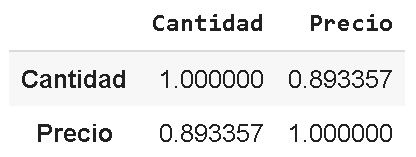
En un caso real un valor tan alto como este sería probablemente muy útil para realizar predicciones.

La función corr devuelve una matriz la cual compara las correlaciones de todas las variables entre sí. Esto es útil, pero generalmente nos interesa hacer predicciones de una única variable, por lo que solo nos interesaría la correlación de esa variable con las demás, es decir, solo nos interesaría una única columna de la matriz. Afortunadamente Pandas nos permite seleccionar columnas al momento de medir correlaciones. Veámoslo con un ejemplo, voy a usar este dataset, el cual guardaré en un dataframe de Pandas llamado df3.

Hasta ahora usamos datasets con pocas variables, por lo que las matrices de correlaciones eran pequeñas y fáciles de mirar. Pero al usar un dataset real vemos que la matriz puede volverse enorme muy fácilmente.

Vamos a ver la matriz de correlaciones de este dataset.

df3.corr() 

Lo que nos da esta enorme matriz, la cual tiene demasiados números para mirar.

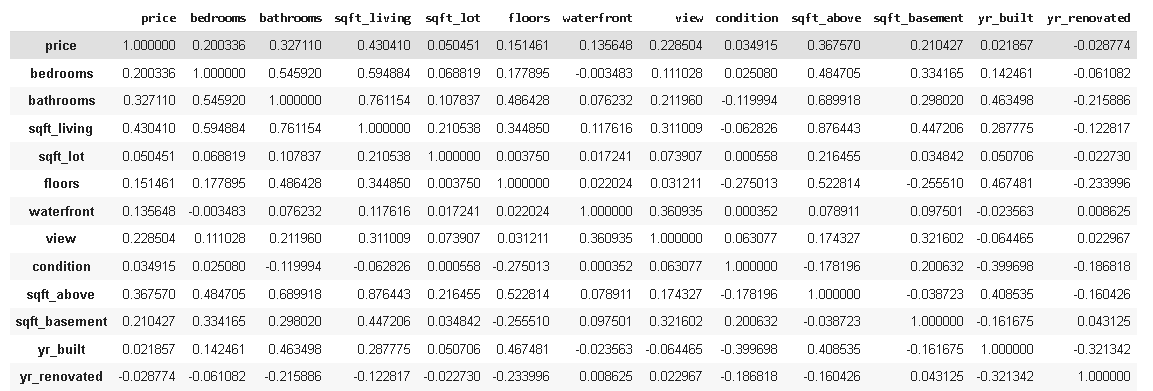
Como mirar tantos números es incómodo, una práctica común suele ser el usar “mapas de calor” al medir la correlación. Básicamente son matrices iguales a esta donde el color de cada cuadro varía según el valor del coeficiente de correlación, haciendo bastante más intuitivo el proceso de encontrar correlaciones fuertes. Los mapas de calor suelen verse así.

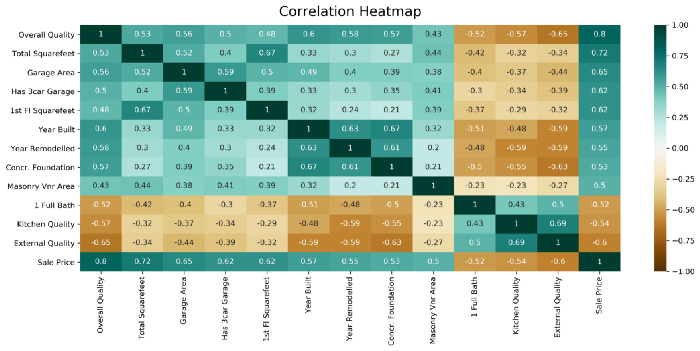
Imagen tomada de este artículo de Medium

Volviendo a nuestra matriz difícil de mirar y sin colores. Sería razonable usar el dataset para predecir el valor de la variable precio. En ese caso, podría ser perfectamente válido el que nos importara únicamente la primera columna de la matriz.

Así que para hacer nuestra vida más fácil podemos obtener únicamente esa columna siguiendo esta sintaxis.

mi_dataframe.corr()['nombre_de_columna'] 

En este caso entonces escribire esto

df3.corr()['precio']

Lo que nos da la siguiente columna mucho más fácil de mirar y entender.

Si queremos ir un paso más allá podemos utilizar tambien la funcion sort_values() para ordenar los resultados de menor a mayor. 

df3.corr()['price'].sort_values()

Lo que nos devuelve lo mismo, pero ahora ordenado de menor a mayor.

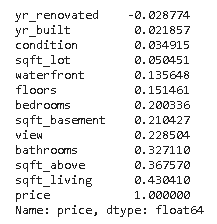
En la segunda parte del artículo sobre regresión, usamos la librería matplotlib para mostrar las correlaciones en una gráfica.